Category: Debate

Rescuing Broken Discourse with Logic

We are in danger. Public discourse is almost dead, with important conversations being shut down by twisted logic resulting in false associations and cancellations. We need to step in and reclaim sanity. This article discusses some of the most glaring logical offenses that are sadly ubiquitous in the global conversation.

Anyone who voted for Trump is a white supremacist.

For many of you, reading that sparked a response charged with negative emotion. Some people probably got so angry they stopped reading and aren’t even here anymore.

Maybe you voted for Trump and took it as an attack. Maybe you hate Trump and got angry because you think the US has been overcome by white supremacists. Maybe you strongly agree with the statement. Maybe you vehemently disagree. There are lots of reactions that statement can instigate. But if it upset you, regardless of why, I offer my sincere apologies.

For the record, I disagree with the statement. In fact, I know it to be false. I’m Canadian, so I didn’t have a vote, but I have more than one personal acquaintance who did vote for Trump, and none of those people are white supremacists. That should be safe for me to say. Yet in many arenas, it isn’t. In many arenas, I would just have caused myself to be written off as a white supremacist too, among many other vile labels – guilt by association with a phantom assumption. And I haven’t even stated who would have gotten my vote if I had one which in any case is irrelevant. What is relevant though is how quickly and completely conversation gets shut down on critically important topics like this one that plague our collective discourse. This phenomenon demonstrates a fundamental lack of understanding, or perhaps worse, a deliberate lack of honouring, some core principles that we study in formal logic, which has roots both in philosophy and in mathematics.

Let’s switch to a less charged example.

Anyone who drinks water is a marathon runner.

It’s silly right? Drinking water does not imply that you run marathons, and to make the claim that it does is clearly ridiculous. What’s less absurd though would be saying that anyone who runs marathons drinks water. But even there, be careful, because there’s an association that many people will make that has nothing to do with why that sentence is true. See, although distance running does require proper hydration, that’s not the reason that marathon runners drink water. A marathon runner is a marathon runner even when they are not running. And they drink water for the same reason non-marathon runners drink water. In fact marathon runners drink water for the same reason all humans, not to mention marine mammals, sea birds and even trees drink water. Because they need it to survive. So if you discover someone drinking water, it’s not likely you would jump to the conclusion that they are a marathon runner. The distinction between “If you are a marathon runner then you drink water” and “If you drink water then you are a marathon runner” highlights the difference between what formal logic calls implications and their converse. It’s important to understand this concept, so let’s work on a short lesson.

First, we need to understand what we mean in formal logic by a statement.

Definition of “Statement“

In formal logic, a statement is a sentence that has a definite state of true or false. Some examples:

“Justin Timberlake is older than Justin Bieber.”
(provably TRUE statement)

“5 is an even number.”
(provably FALSE statement)

“‘5 is an even number’ is a statement.”
(humorously constructed TRUE statement)

“There is sentient life on other planets.”
(Definitely either TRUE or FALSE, but although I have a guess, I have no proof that I’m right)

We can not always tell if a statement is true.

Although it’s fairly easy to tell if a sentence is a statement, it’s often difficult or even impossible to tell if it’s true or if it’s false. The statement “There is sentient life on other planets” does have a definite truth value, though we can only guess at what that value might be. And that’s where opinion enters the arena. Now consider this much more highly charged statement: “An unborn fetus is not a living human.” I bet that one sparked some intense emotion in many readers. And I’d also be willing to bet that the emotion it sparked is tied to your opinion about whether or not it is true.

That’s just your opinion

Guessing at the truth value of a statement is my preferred way to define opinion. We can argue over what we think about aliens from other worlds, or when human life begins, but until we have evidence that proves or disproves our position, all we are doing is voicing opinion. Isaac Newton said it well:

(We) may imagine things that are false, but (we) can only understand things that are true, for if the things be false, the apprehension of them is not understanding.

Isaac Newton

So we can apprehend (consider in our thoughts) beliefs and opinions, but false is false, so any belief attached to a false thing is not true understanding. Compounding the problem this highlights is that it is human nature that purging a disproven belief requires a deliberate and often painful reorientation, so often what we see is denial, and a loyalty to a false opinion. It might be human nature, but it’s dangerous.

Consider this thought experiment:
Suppose you are pro-choice, because you indisputably support the right of a human to make decisions about their own body. It would likely (but admittedly not certainly) then be the case that you also believe that the fetus is not a human, and so there is no conflict between the rights of the mother and the rights of another human. Then suppose you learned, conclusively, that a fetus is a human baby, effectively equating abortion with homicide. How would that make you feel? Would it be easy to change your position? In this thought experiment, where the premise is that it has been proven that a fetus is a baby, would you choose to deny that truth?

It’s an extremely difficult thing to think about dispassionately. But beware when asserting opinions as facts, and be prepared to understand that until a fact is known/proven, your opinion will differ from that of others, and arguing with them without establishing that both arguments are predicated on opinion is more of an exercise in charisma than debate.

Opinion Vanishes in the Face of Proof

Once the truth value of a statement is established via proof, opinions are rendered irrelevant, and they only persist as the result of deliberate obstinacy, miseducation/delusion, or in many cases, indoctrination. Interestingly, this applies even if your opinion happens to align with the truth. If it is your opinion that there is sentient life on other planets because you believe Star Trek is a documentary, then even if there is sentient life on other planets your opinion is based on delusion, and the fact that you are correct is coincidental. Think of it this way: If you’ve been maintaining that there is life on other planets because Captain Kirk fought a Gorn, and one day life is discovered on another planet, you would look pretty foolish proclaiming that you were right all along. So whether “correct” or not, opinions are just opinions. It is interesting to consider the ramifications of using miseducation to deliberately delude uneducated people into having an opinion that aligns with the truth, but maybe that’s a topic for a different article.

Ok, so hopefully we understand now that a statement is either true or false, and that we can’t always know which it is. Furthermore, if we guess, then we are forming opinions. This gets even more interesting (if that is the word for it) when we create compound statements by linking statements conditionally. Like saying “If you voted for Trump then you are a Nazi.” Using If/then to link statements is called implication. We use them a lot.

Definition of “Implication“

“If you are reading this article, then you understand English.”

Is that true? I think so. In any case, that statement is an example of an implication – a compound statement that conditionally links two statements. Implications claim that if we know that one statement (called the predicate) is true, then we can conclude that a second statement (called the conclusion) is also true. Even though implications don’t always present the same way, they can always be formulated using “if/then”.

Because implications are statements, they will either be true or false. For example:

Predicate: I was born before 1970
Conclusion: I am older than 30
“If I was born before 1970 then I am older than 30”
True – based on arithmetic

Predicate: A person is wearing pants
Conclusion: That person is hungry
“If a person is wearing pants, then that person is hungry”
False – a person who was wearing pants and was hungry, who has just eaten their fill, will still be wearing pants (though they may have unbuttoned them!)

Any statement that can take the form “If A, then B“, which is to say “A implies B“, is an implication. For example:

“All football players use steroids”

can be reformulated as

“If you are a football player then you use steroids.”

It is worth noting that the above statement about football players is an example of a false implication, even though it is the opinion of many. Unlike opinion, truth is not ascertained or even swayed by consensus.

It’s also important to distinguish between the truth of an implication, and the truth of the conclusion. For example, “If I win a hundred million dollars in the lottery then I will buy a Lear Jet.” is a true implication (ask my wife – we’ve discussed it), but it does not mean I am going to be buying a Lear Jet. When “A implies B” is true, it doesn’t mean B is true, or even that B could ever be true. It just means that if you observe that A is true, then you can conclude that B is also true. This connection actually has a cool Latin name in formal logic. It’s called Modus Ponens.

Modus Ponens

Modus Ponens is a special implication that we use to make deductions by citing established implications. It says “If A implies B, and A is true, then B must also be true.” A very common error is when people pervert modus ponens into “If A implies B, and B is true, then A must be true.” This is faulty. Consider this example:

“If you stick your hand into a toaster while it’s on, you will burn your hand.”
This is true.

Now consider these two arguments:

Modus Ponens
“I see you stuck your hand into a toaster while it was on. You must have burned your hand.”

Faulty Deduction (perverted Modus Ponens)
“I see you burned your hand. You must have stuck it into a toaster that was on.”

This perversion of modus ponens can also be dangerous. Imagine the implication “If you are racist then you supported Trump” is true. Now consider this faulty deduction: “I see you supported Trump. You must be a racist.” This is precisely the sort of perverted logic that divides and fragments society, potentially irreparably.

This leads us to the notion of the converse of an implication, and the contrapositive.

“Converse” and “Contrapositive”

Every implication has a converse and a contrapositive. The converse switches the predicate and the conclusion, so the converse of “A implies B” is “B implies A“. On the other hand, the contrapositive of “A implies B” is “not B implies not A“. The contrapositive means that if you know the conclusion is false, then you can conclude that the predicate is false. It’s essentially saying the same thing as the implication, in a different way. That argument has another cool Latin name: Modus Tollens:

Modus Tollens

Like Modus Ponens, Modus Tollens is used to make deductions using established implications. It says “If A implies B, and B is not true, then A must also not be true.”

Consider this example, which demonstrates the ideas of implication, contrapositive, and converse. Suppose you took a Spanish course where students who fail earn a grade of F:

Implication:
“If I got a C, then I passed the course.”
(True – A credit is awarded for any grade other than F)
Modus Ponens: ” I see that you got a C, so you must have passed the course”

Contrapositive:
“If I didn’t pass the course, then I didn’t get a C.”
(True – not passing – i.e., failing the course, means you got an F)
Modus Tollens: “I see that you failed the course, so there’s no way you got a C.”

Converse:
“If I passed the course, then I got a C.”
(False – You may have gotten an A, B, C or D.)
Faulty logic: “I see you passed the course, so you must have gotten a C.”

Notice that the implication is true, the contrapositive is also true, but the converse is false.

Sometimes the converse is true, and sometimes it is false

For true implications sometimes the converse is true:

“If we have a common biological parent then we are biological siblings.”
has the converse
“If we are biological siblings then we have a common biological parent.”

and sometimes it isn’t:

“If our fathers are brothers then we are cousins.”
has the converse
“If we are cousins then our fathers are brothers.”

So knowing an implication is true does absolutely nothing to tell you if the converse is true – or false. Yet there is a strange insistence in public discourse that true implications always have true converses. This is glaringly demonstrated in political discourse.

How would anti-immigration voters have voted?

Consider this implication, which may or may not be true (probably is), but many readers will definitely have an opinion about it:

“If you are racist then you will not hire a black candidate.”

Now consider the converse:

“If you did not hire a black candidate then you are racist.”

I have heard this claimed countless times. And there’s no logical foundation for it. This highlights another common error people make. Implications create links (being racist links to not hiring black people), and people then use those links to try and reverse-engineer a converse (not hiring a black person links to being racist). This can be attributed to the notion of ruling out. Suppose that all immigrant-haters voted for Trump, and that you did not vote for Trump. Then using Modus Tollens I can rule you out as an immigrant-hater (you did not vote for Trump, so you must not hate immigrants).

However if you did vote for Trump, then I can’t use Modus Tollens or Modus Ponens to disprove (rule out) the possibility that you hate immigrants, because in the implication we are citing, hating immigrants is the predicate, not the conclusion, and all I have observed is the conclusion. So your position on immigrants is something I’d have to look at other factors to determine.

Not being able to disprove a statement does not mean it’s true

True: “If you get a D in Spanish, then you earn a credit.”

Suppose you believe that I got a D in Spanish. Now suppose that in an attempt to prove that you are correct, you do some digging into the school records and discover that I did take Spanish, and that I earned a credit. Does that mean I got a D? You can’t tell. All you know for certain is that I am in the group of people who earned a credit. You hopefully also know that anyone who earned an A is in that group. Me being in the same group of people who earned a D is not proof that I earned a D, because all the credit-earners are in that group, and they did not all earn D’s. You could say that you have gathered some evidence that I earned a D, but you can not say that you have proven it. So you have neither proven nor disproven your belief. On the other hand, if your digging showed that I took the course but did not earn the credit, Modus Tollens rules out the possibility that I got a D, and your opinion is false. Which is to say, “You did not earn a credit, therefore you did not get a D”.

So then if it’s true to say that immigrant-haters voted for Trump, and you know your coworker voted for Trump, then all you know is that your coworker is in the same group as immigrant-haters. Now even though you can’t rule it out, you can not conclude that your coworker hates immigrants. So if you start a conversation with them by accusing them of hating immigrants, that’s bound to go poorly.

Implication does not imply causation

We also need to think about a common misconception, which is that true implications are therefore causations. That’s the false belief that if we know that “A implies B” is true, it must mean that “A causes B”. This is actually just another example of mistakenly believing a converse:

“If A causes B then A implies B” is an implication where the conclusion is also an implication, and it’s true.

The converse, “If A implies B then A causes B” is false.

Consider this example, which has embedded causation:

Let A be the statement “Your car has no fuel” and
Let B be the statement “Your car won’t start.”

So:
not A is the statement “Your car has fuel” and
not B is the statement “Your car will start.”

Implication (If A then B):
“If your car has no fuel then it won’t start.”
(True – Cars with no fuel won’t start, and even if there are other things wrong with the car that we don’t know about, knowing it has no fuel allows us to invoke causation to conclude it won’t start)

Contrapositive (If not B then not A):
“If your car will start then it has fuel.”
(True – You can’t start a car if it has no fuel)

Converse (If B then A):
“If your car won’t start then it has no fuel.”
(False – there are lots of reasons why a car won’t start and being out of fuel is only one of them)

… which brings me to strength-training.

What Does This Have To Do With Strength Training?

The car example shows that even when causation is the reason an implication is true, we still don’t get the converse. But sometimes the example in question is less clear, and people jump to conclusions.

For example:

Truth Due to Causation:
“If I participate in a strength-training regimen at the gym, then I will get stronger”
(True because of the causal relationship between strength-training and getting stronger)

So we have an implication that is true because of causation. The converse is “If I got stronger, then I participated in strength-training at the gym”. That’s a conclusion people jump to all the time. “Oh, you have gotten stronger – you must have been working out!” False. Lifting weights in the gym is not the only way to get stronger. Someone who gets a job that requires heavy lifting will also get stronger. Children get stronger just by growing. So if you find someone who has “gotten stronger” you cannot automatically conclude that they started a strength-training program at the gym. Again, even when there is causation, a true implication is not proof that we have a true converse.

It’s time to bring this back to public discourse. It’s crazy-making to see how many people seem to think that the converse is always true. Or if not, they pretend they do, to fool others into buying an argument. Let’s look at an extremely charged example: rape.

All rapists are men

This isn’t technically true, but while a very small percentage of rapes are not perpetrated by men, the vast majority are. This is a horrible truth. One that has troubled me since I was old enough to have learned it. As a thought experiment, let’s simplify this and for a moment assume that all rapes are committed by men. So then we would have this implication:

“If you are a rapist, then you are male.”

But consider the converse:

“If you are male, then you are a rapist.”

I hope we can clearly see that the converse is false. Sadly, I have heard this converse claimed (or implied) many times, and it does nothing at all to help the real issue of rape. Good people want to eradicate rape, because rape is monstrous, and good people want to reduce suffering. Taking good men and lumping them in with bad ones by claiming masculinity as the driving force behind the desire to rape, creates extra suffering. It makes no sense.

There are many other places where we see the converse invoked dangerously. One chilling example is when someone asserts that an implication is true, but then get accused of having supported the converse. This then changes the conversation about a potentially difficult issue into one of accusation and defense.

I will list some examples of implications I have heard claimed, where an immediate switch to the converse then changes conversation to the wrong topic. As an exercise, in each case, state the converse of the implication in your mind and ask yourself what trouble that might cause, and how it would poison the (potentially difficult) conversation. As I said, these are heavily charged statements. In many, if not all cases, the reason they are heavily charged is probably not the implication, but what the converse would mean, if it were true.

I feel that I have to repeat that I am not claiming the implications in the examples are true, though I know they are the opinion of many. But if they are true, it’s because they are, and if they are not, it’s because they are not. Opinion vanishes in the face of knowledge. Still, arguing about the converse has nothing to do with either of those cases and changes the dialogue into something irrelevant. It’s important, as you read, to keep the dispassion of viewing claims through the lens of formal logic. For each implication, consider what it would mean if it were true, and whether the converse would then also apply.

Do you think any of these are true?
Do you think their converse is true?

  • If a person is a white supremacist, then that person would have supported Trump over Harris.
  • If a person is a mass killer, then that person is a gun owner.
  • If a person is a member of Hamas, then that person is Muslim.
  • If a person is misogynist, then that person is male.
  • If a person is a stalker, then they will like all your photos on Instagram.
  • If someone wants to rob you, then they will walk behind you at night.

Do you think any of these are true? If so, do you also think the converse is true? If you think the converse is true, is your evidence of this that the original claim is true? If so, you have no foundation to back the claim to the converse. Seriously. None. Hopefully this article has made that clear.

Just because an implication is true, it does not mean its converse is also true.

And yet there seem to be a huge number of people out there who think that it is impossible to hold to a claim and not hold to the converse. For example they think that if you talk about mass killers being gun owners then you want to paint all gun owners as mass killers – which is a ridiculous notion on so many levels, perhaps the most obvious being the staggering number of gun owners who are not killing anyone with them – and they label you as ignorant, or as a fear-mongering anti-freedom fanatic with a hidden agenda. But there is simply no logical foundation for this connection. What they are doing, from a logical perspective, is saying that since you believe an implication is true, you also believe the converse, and so you are pushing a hidden agenda. And I just can’t say how many ways this is wrong, and dangerous.

“But wait!” some say, “fear-mongering anti-freedom fanatics pushing a hidden agenda DO say that most mass killers are gun owners! So by saying that aren’t you one of them?”

Once again, they are invoking the converse of an implication, possibly without realizing it – though I suspect in some cases fully realizing it and doing so anyway to redirect away from rational discourse. “If you have a hidden agenda then you will say that most mass killers are gun owners” is not the same as “If you say that most mass killers are gun owners then you have a hidden agenda”.

To illustrate just how silly all of this is, I’ll talk a little about probability, using Venn Diagrams. This time we’ll talk about serial killers.

Most Serial Killers Eat Breakfast

This is an implication, but what’s not immediately obvious is that it invokes a probability statement due to the word “most”. It means that if you encounter a serial killer, then they probably eat breakfast.

Because of how we use the word most, it arguably means anywhere between 50% and 100%, so for the sake of argument, let’s suppose that 80% of serial killers eat breakfast. I’m sure that number is low, but I’m thinking that if I attempt to consult studies on the eating habits of sociopathic murderers, I may find limited data has been collected. In any case, assuming 80%, a visual representation might look like this:

Venn Diagram 1

So if you want to bet on whether a particular serial killer eats breakfast, and you don’t know ahead of time, you should make the bet, because you will probably win.

Now consider this Venn Diagram: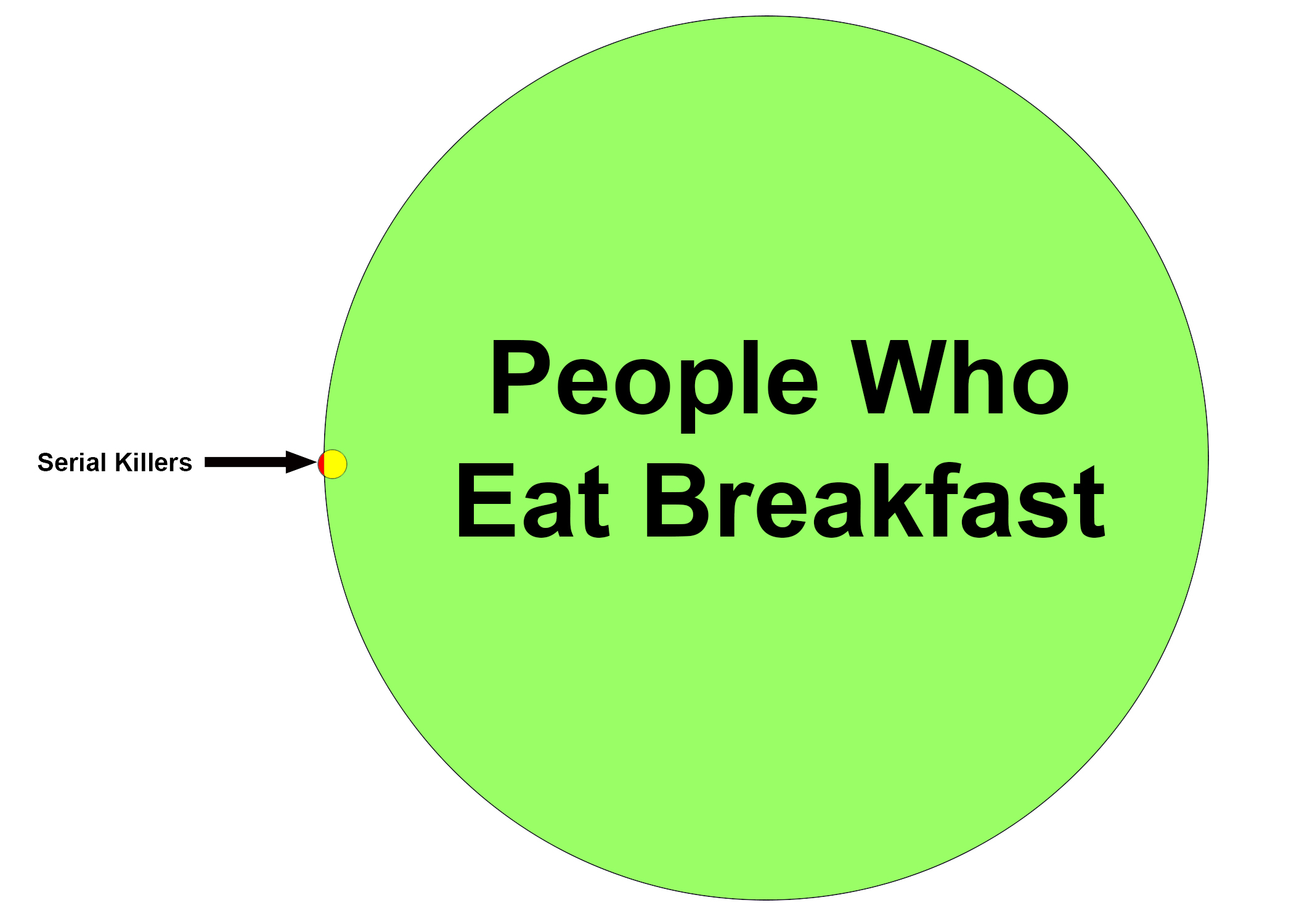
Venn 2.jpg
Even though the green circle isn’t nearly large enough (if it were, we wouldn’t even see the yellow part), this still demonstrates that most people who eat breakfast are not serial killers. Think about how much green there is compared to how much yellow. So if you came upon someone eating breakfast, you should be pretty confident that they are not a serial killer, keeping in mind that it doesn’t constitute proof that they are or that they are not. I’m thinking that is probably the case for you – that you don’t consider breakfast-eating to be compelling evidence of evil.

Being in the same group as someone does not mean you share all the same qualities

When someone says or does something that a serial killer, (or a racist, a rapist, a transphobe, a misogynist …) might do, it is false and dangerous to conclude that that person is one of those evil things. Notice the italics on the word might. That’s a probability word. A rapist might have eaten breakfast today. So might a non-rapist. And there are way more of those. To call someone a rapist, you would hopefully be using evidence they had raped someone, not evidence that they had eaten breakfast.

Or evidence that they are male.

Bad People Can Say True Things

It’s true. Truth is not the sole domain of the virtuous. Truth, in fact, like justice (purportedly) is blind. And it’s critical that we do not devalue the truth of a statement just because it aligns with the opinion of someone nefarious.

For example, someone who hates Muslims would be willing to assert that most suicide bombers have been Muslim, because it would further their agenda of hate, especially for those who immediately jump on the converse, which is clearly absurd. But if the claim is true, then a rational thinking non-racist could also say it. To then say “well islamaphobes say that, therefore you are islamaphobic” is to claim a converse that isn’t true. What’s far worse is that the label shuts down conversation. And if we can’t talk about things that are problematic, like racism, mass shootings, terrorism, sexual assault, or a myriad of other difficulties we face in modern society, how can we make things better? We can’t.

Good People Should Say True Things

Especially when it is hard, and even if it coincidentally aligns with the opinions of assholes, it is critical to acknowledge true things as true. Good people want to reduce misery in the world. Good people want to increase happiness in the world. Please don’t use the trick of claiming the converse to stand in their way. Let’s allow honest discussion to flow.

Thanks for reading,

Rich

Revolutionizing Social Media Interaction for a Brighter Future

As we get closer to the American elections, and then moving into the Canadian elections next year, I find it more and more imperative that we work to effect a fundamental change in the way we interact with social media and, by extension, how we interact in real life. Over the last ten years or so my concern over the culture has grown from mild alarm at some people’s online behaviour, to something approaching real fear that we are at a tipping point into another real-world dark age, specifically with respect to intellectual and cultural decline. And violence.

It’s not all bleak though. Thanks to many private conversations, I know I am not alone in my concern, and I do see signs that there are public figures with a legitimate desire to change this trajectory, as opposed to leveraging the culture for their own personal gain. And considering the magnitude of people who, exclusively through social media, get their news, form their opinions, and – maybe most troubling – learn how to communicate, social media is where it has to start.

If we can do it, it won’t be through any kind of censorship or similar attempts to control how people use their favourite platform though. It has to be you and me. We have to change the nature of our posts. And so I had this idea of a filter, or sieve, that we can apply to our more meaningful posts to both increase their effectiveness, and also combat the culture that is propelling us toward a precipice.

Consider this. If you want to engage in political posts on social media, that is your choice, and I support it. Keep in mind though that these posts are, by nature, argumentative, in that political posts always argue for or against some candidate or issue. Which on its own is not a problem. Argument (or debate) is not a fight. The idea that arguing equals fighting is something that’s manifested because people like getting attention and scoring points. True argument is not a contest, but a means to pursue truth and, conducted properly, is how we progress. Because the acquisition of truth can never be considered a loss, proper arguments have no losers, and in that sense they have no winners either, because to win an argument someone would have to lose.

But many people argue poorly, because they argue for points.

In the philosophical study of argument there are many identified fallacies. If you’re not familiar with the idea of a logical fallacy, think of these as techniques or strategies that falsely trick you into thinking they are effective. When you employ them you or your audience may think you’re “winning” but you have not made a true case. To avoid this, and hopefully steer us away from the precipice, I ask that you apply what I’m calling an effectiveness sieve to your words before you click that post button.

Run your post through the following sieve. If you can’t answer yes to all three sieve questions, refine your thoughts until it passes them all, then go ahead and put it out there.

  1. Do my words avoid belittling, shaming, or otherwise personally attacking someone who doesn’t agree with my position?
  2. Does my post allow for (and even maybe invite) respectful discourse with someone who disagrees with it?
  3. Does my post offer information/education that someone who disagrees with me might not have considered?

You can actually stop reading here, if you like. The value of each question is probably self-explanatory. But if you want to dive a little deeper into the reasoning behind these criteria and their relationship to common fallacies, or to reflect a little more deeply on whether or not your own posts are effective, read on.

(A word of warning though: I use examples below to illustrate the points and a lot of them are, by design, inflammatory in concept and language. I am not expressing my views in any of them – I am parroting posts I have seen in my social media feeds.)

Sieve Question One
“Do my words avoid belittling, shaming, or otherwise personally attacking someone who doesn’t agree with my position?“

Fallacy This Helps Avoid: Ad Hominem (Attacking the person)
This occurs when instead of challenging an idea or position, you irrelevantly attack the person or some aspect of the person who is making the argument. The fallacious attack can also be aimed at a person’s membership in a group or institution.1

How to tell
Imagine that someone who holds an opposite position made a post worded like yours. Would you take it as a personal attack, or would you view it as someone simply supporting ideas that you disagree with? Keep in mind that we can challenge ideas without attacking the people who embrace them. In fact, this is the only way to dismantle dangerous ideologies. In democratic societies where change essentially requires consensus, attacking opponents instead of ideas is possibly the worst way to stimulate progress. Consider this example:

Example 1
“Considering the unbelievable depths of stupidity you display in believing that climate change is a hoax, it would obviously be a waste of time explaining the facts to your fascist republican ass.”

Example 2
“You have been duped by the lamestream media, so I will leave you to your weak-minded, sheeple liberal delusions about how solar power will ‘save the planet'”

Example 3
“I read conflicting views on whether climate change is real, if it is a concern, and if it is totally caused by human factors. I am not an expert, and it’s not always easy to filter out the real experts from the ones who claim to be. And even then, it’s not always easy to filter out which experts, if any, are twisting their analyses to suit some underlying agenda. However, the scientific consensus points at climate change being a real danger, and being attributable to human factors. The recommendations to address it seem to be a net good, even if the premise that we are the problem isn’t totally correct.”

It should be obvious what’s happening in the first two examples. There is no attempt to change anyone’s mind. It’s just mud-slinging peppered with tired insults engineered to pump up the audience members who agree. Neither post does anything to address the issue of climate change itself, and just drives a wedge between people who hold opposing views.

Meanwhile, if I’ve crafted the third example well enough, hopefully you can see that there is no evidence of ad hominem at all, and even though the poster is leaning toward one “side”, they have not shut down engagement.

Sieve Question Two
“Does my post allow for (and even maybe invite) respectful discourse with someone who disagrees with it?“

Fallacy This Helps Avoid: Straw Person
This occurs when, in refuting an argument or idea, you address only a weak or distorted version of it. It is characterized by the misrepresentation of an opponent’s position to make yours superior. The tactic involves attacking the weakest version of an argument while ignoring stronger ones.2

How to Tell
This is often used in conjunction with the ad hominem fallacy because it adds even more punch. After all, only moron would believe a weak argument. Most people have no desire to engage in discourse with someone who starts off with the premise that “Your position is weak, because it supports x so I am right and you are wrong and unless you can see that you are an idiot.” Consider the contentious example of abortion:

Example 1
“Pro-choice? So you think that murdering babies is ok!?! I guess you don’t care about the lives of the babies who get killed.”

Example 2
“Pro-life? So women should have no say over what happens to their own bodies?!? I guess you don’t care about the 13-year old girl who was brutally raped and is now forced to carry and give birth to the child of the man who scarred her forever.”

Example 3
“I struggle with the abortion issue. I believe it is a clear and terrible breach of fundamental human rights to tell someone else what they can or can’t do with their own bodies, regardless of the circumstances but especially when there is physical/psychological trauma involved that can be addressed with an abortion. But I am also really troubled by the fact that I am in no position to decide whether a viable fetus, at any stage of development, is a human life, and I don’t see how anyone could be, really. The issue feels like being offered only two choices where each choice is loaded with ethical downsides, and there is no option to not choose. I worry that in order to alleviate the moral weight of each choice, people downplay or even outright lie about the consequences of their position. So although I land on the side of pro-choice, I do not do so lightly, and I am aware that it feels like I have made a moral choice to prioritize the essential rights of the mother over the potential rights of the unborn child. I hope this choice is correct.”

Consider the first two examples. Will a pro-choice person who just got told they murder babies want to engage in anything other than hurling insults with this person? Will a pro-life person who just got told they don’t care about the effects of rape on a 13 year-old girl want to engage in anything other than hurling insults with this person? By attacking a weak/distorted version of the other side, each has set it up so that any engagement by someone with an opposing view will manifest as some level of support for the weak/distorted claim.

Meanwhile, in the third example, the author has ultimately stated a position. Would a pro-x person be open to understanding the author’s struggle? Would a pro-life person feel safe to engage in discourse? Does it seem that there is the possibility that anyone who engages – including the author – might change their minds about anything surrounding the issue, including about people themselves who hold the opposite position?

Sieve Question Three
“Does my post offer information/education that someone who disagrees with me might not have considered?“

Fallacy This Helps Avoid: Irrelevant Authority
This is committed when you accept, without proper support for an alleged authority, a person’s claim or proposition as true (and that alleged authority is often the person employing the fallacy). Alleged authorities should only be referenced when:

  • the authority is reporting on their field of expertise,
  • the authority is reporting on facts about which there is some agreement in their field, and
  • you have reason to believe they can be trusted.

Alleged authorities can be individuals or groups. The attempt to appeal to the majority or the masses is a form of irrelevant authority. The attempt to appeal to an elite or select group is also a form of irrelevant authority.3

How to Tell
Are you claiming that some position is wrong? If so, have you explained how you know this? What authority are you citing? Or are you claiming expertise and asserting “Thinking x is wrong!”

Example 1
“Jordan Peterson says switching to a meat-only diet literally saved his life. Vegans are slowly killing themselves.”

Example 2
“I lost 30 pounds when I went vegan and feel so much better. Eating meat is asking for heart disease and dementia.”

Example 3
“It makes sense to at least consider evolution when determining what a ‘healthy’ diet looks like. Before humans had access to foods not native to our geography, the only people that would have survived would be the ones who thrived on what was available. So if your ancestors evolved in warmer climates, it would make sense that your constitution would welcome more grains and vegetables, whereas ancestors in colder climates would have evolved to thrive off meats.”

Consider the first two examples. Jordan Peterson is not an authority on nutrition (he actually takes great pains to make that clear whenever he talks about his diet). So while he has said that a carnivore diet works for him, it is not evidence that the carnivore diet is better than others. In the second example, the author is actually setting themselves as the authority. Neither example offers any warranted expertise or education and are strictly anecdotal claims.

In the third example the author poses an idea that promotes questioning and further research. They are not claiming any personal authority, or even choosing a side, even though they may have a preference. They are presenting an hypothesis that can be (and probably has been) analyzed by experts.

If you’d like to read more about informal fallacies often used in argument, I recommend this link from Texas State University. It lists the common ones and provides explanations and examples. One of my favourites is Begging the Question, which I always laugh about because it’s a phrase that gets used so often, and almost always incorrectly, while at the same time the real fallacy gets used regularly in arguments.

In any case, I hope we can all change the way we interact on social media and beyond. I really do believe we need that flavour of revolution.

Thanks for reading,
Rich

  1. https://www.txst.edu/philosophy/resources/fallacy-definitions/ad-hominem.html ↩︎
  2. https://www.txst.edu/philosophy/resources/fallacy-definitions/straw-person.html ↩︎
  3. https://www.txst.edu/philosophy/resources/fallacy-definitions/irrelevant-authority.html ↩︎

Why Study Mathematics?

In my job, this question is one I get asked very often. To be honest, it usually comes in a slightly different form …

“When am I ever going to use this? What is it good for?”

As a high school math teacher for 15 years, this is one of the most common questions I received. When I began lecturing at university, I was surprised to find that I still sometimes get asked variations of this question. I suppose it’s a good question, if the idea is that at some point someone will say to you

“Determine

and have your answer on my desk by 5pm today. And don’t get any funny ideas about using WolframAlpha!”

Because the truth is, that rarely happens.

I often give a joking answer, and say flat out, “You won’t,” and then go on a rant about how math doesn’t need to be good for anything, because it is just good. Nobody ever stood in the Sistine Chapel, staring at the ceiling, asking what it was good for! They just appreciate the inherent beauty, because it speaks to their soul. Math is the same.

I think that’s a perfectly good answer, to be honest. But in a more serious light, I find the answer to the question is actually another question: “When are you not going to use this?”

Of course, there are direct applications of many branches of math. But those tend to be very specific, and these days depend heavily on software to do the heavy lifting, so I tend not to think of those. Instead, consider that football players perform bench press as part of their training, to the point that the ability to bench press 225 pounds for as many reps as possible is tested at the NFL combines. Yet not once have I ever seen a football player perform the bench press during a game. Why do they do it then? Couldn’t they just practice the skills they will actually use in a game? I can promise you that at no point during a football game does a player think “oh, this situation is just like bench pressing 225 pounds – I will apply that same skill now.” And I imagine there are very few football players who complain while lifting weights that they will “never use this in real life”. Of course, we know that the reason they train the bench press is that it increases strength and power, so that when the time comes that they need it, it will be there without consciously calling upon it.

Studying mathematics is the same. Math teaches so much if we are awake to the lessons. Here are some things I have learned, continue to learn, and apply regularly from my math studies, along with some examples of how they have impacted me personally.

Scale simple solutions to solve large problems

It is almost always the case that large problems can be effectively solved by breaking them into smaller problems, or by developing scalable solutions to simpler problems. For example, about 3.5 years ago I decided I wanted to learn to draw, so I took a piece of white printer paper and a mechanical pencil and drew a superhero-esque muscle man. It sucked. Like a lot. But I was not discouraged in the least by that. I was fueled by it. Why does this suck so much? I know how I want it to look, why can’t I make it look that way? I was excited by the fact that I could recognize how much it sucked, and by the prospect of working to slowly strip away the suckness. I spent hundreds of hours, solving small problems that were contributing to the suckyessence, and slowly scaling them up. Want to draw a heavily muscled arm? Learn to draw a cylinder. Then learn to draw little cylinders that lie on the main one. Then learn to draw “twisted” cylinders and tubing that changes diameter as it twists. Learn anatomy. Now put it all together. I intuitively understood platonic solids and how they interact with and reflect light. I applied these understandings to understand the types of skills I needed to hone with the way I held and manipulated pencils. I started looking closely at things I never paid attention to before. I still do this, and at no point during this process do I ever consciously say “Oh, that’s just like <fill in math course here>”, but at every point I feel exactly the way I feel when I am working on difficult math problems.

Being right also means proving you are

Math is really never about just “getting the right answer”. It’s about proving that an answer – or a result – is correct. The emphasis on proof is critical. In the real world, being right is rarely enough if you can’t convince others that you are. Careful, methodical, and audience-appropriate explanations are invaluable in this regard. Developing and writing proofs in mathematics is as much an art form as it is a science (perhaps even more so), and my studies in mathematics immeasurably improved my approach to constructing an audience-appropriate argument or explanation. This has had a profound impact on my communication skills, as well as my approach to confrontation. I have used this skill in more ways than I can list, but some examples are: when I have been in contract negotiations, when I deal with sales people when buying big-ticket items (and even when I bargain at markets), when I find myself moderating arguments between friends, family, colleagues or students, and when I used to work as a personal trainer and had to motivate and justify the kinds of exercise and diet choices I wanted my clients to make. In every single one of these situations, and more, I am really constructing proof. In fact, I would say that proof dominates almost all my communication.

Emotional attachment to a belief is irrelevant

Not wanting to be wrong about a belief, especially if it has been long-held, is normal. It is, however, illogical and possibly even dangerous in the face of proof to the contrary. Mathematics trains us to seek, understand and ultimately accept proof on its own merit, and not on any emotional yearning. It also trains us to be grateful when proven wrong, since it makes little sense to want to be wrong for even one moment longer than necessary. My training in math has led to a much more open-minded approach to new thoughts and ideas, and after careful consideration – which involves listening to argument dispassionately, asking relevant questions and weighing evidence – I find myself either happily embracing a new thought, or else more confident in the one I already had, having had the opportunity to test it rationally against a differing viewpoint.

Creativity and math are NOT mutually exclusive.

Not even close. Deep study of mathematics reveals and refines a strong creativity that aligns with and is mutually supportive of logic. This fusion is relatively rare, and people who have it are prone to what seem to be exceptional accomplishments. In truth, the exceptionality of it is not the accomplishment itself but the relative scarcity of people who can do it. One of my favourite examples is Leonardo da Vinci, who most people think of as a great artist, but who was also an accomplished mathematician and scientist, and who did not consider these as separate pursuits or modes of thinking. I find the same is true in my own life, although there are many people who wonder how a mathematician could be artistic.

Clarity lives just on the other side of contemplation

The journey math students regularly take from being completely mystified and often intimidated, to understanding and comfort is a lesson in overcoming that serves us well in all the challenges the future can bring. It instills a confidence that says, “I may not understand this right now, or even feel like I ever could, but I know I can do it.” General wisdom suggests that “easy” might seem gratifying in the moment, but true satisfaction comes from overcoming a challenge. Many people shy away from challenge for fear of failure, but studying mathematics teaches us that we can tackle large problems, even if they seem overwhelmingly daunting at the outset. An example that makes me laugh is the time I purchased a large and intricate piece of exercise equipment for my home gym (a functional trainer/smith machine combo). I bought it used, so it did not come with any assembly instructions, and perhaps embarrassingly, it didn’t occur to me to use Google. When I picked it up the seller had already “helpfully” disassembled it into n pieces, where n is large. I was completely baffled at how to reassemble it when I got it home. But I was not daunted. I laid all the pieces out on the floor, shuffled them around into sensible groups, and slowly assembled sections that made sense. I made mistakes and discovered them when they led to chaos. I backed up, took a different approach, and eventually put it together. The process was not “clean” – I hurt my hand trying to brace a nut while tightening a bolt, and cursed myself for not taking the time to get a wrench to hold it in place. But the result looks like it was assembled by a pro. I’ve had it for many years now, and it still works perfectly. I am fully aware that my engineer friends would consider this a trivial exercise, but for me it was a hard-fought and well-earned victory. This type of approach has stood me well time after time.

You don’t always have to see the whole path to the goal

How often have you been working on a difficult proof or problem, not really knowing if you were getting anywhere good, nevertheless continuing to take small, logical steps – always forward, occasionally pausing to reorient yourself to see if the direction made sense – when suddenly you found yourself having completed the entire thing? Some mathematicians call this the “follow-your-nose” principle of proof. A leads to B which leads to C etc. This might be the most important lesson of all. If you have a long-term goal that seems incredibly distant and perhaps overly ambitious, consider that if you just point yourself in the right direction and take small steps, occasionally reorienting yourself, you do eventually get where you want to go. Plus, the journey is so rewarding. In my life I have used this principle I learned from proof over and over and is in fact how I ended up lecturing at university, something that has been a dream of mine since the 12th grade.

And that concludes my very long answer to the common question! I hope you found something of value.

Thanks for reading!

Rich

Open-Mindedness

Recently I have been thinking a lot about why so many people seem inconvincible of certain things which I hold to be true. And while I could certainly make a list of some of these things, that is not the intention of this blog entry. Instead, I have been reflecting on open-mindedness and wanted to share.

Many people – myself included – often enter into discourse with someone of a differing opinion with the intention of convincing them to change their mind. For example, maybe your friend Paul thinks all trees in your neighborhood that are taller than 12 feet should be pruned to 12 feet or less, so as not to obstruct anyone’s view of the lakefront. You know that he’s clearly wrong! You get into a discussion. Only it’s not really a discussion – it’s an argument each of you is trying to win. Maybe out of frustration you start incorporating personal attacks. Maybe you get so angry at Paul’s refusal to capitulate, as well as the horrible things he is saying about you, that it ends your friendship. Maybe in the middle of the night, Paul prunes all of your tall trees. Maybe the next night you erect a 30 foot statue on your lawn directly in Paul’s line of sight to the lake … and so on.

It’s sad, and you don’t even like the statue, but what choice is there? Paul must be taught a lesson.

I wish this was hyperbole. Sadly, it is not. And the conclusion is clearly suboptimal.

Well … let me construct a basis for discussion with some (hopefully) fair assumptions. In doing so I’m going to have to use a little bit of math terminology, and it occurs to me that some people might not know precisely what I mean, or even be put-off by some of my more mathematical references. If you think this might be the case, I ask you to bear with me. The concepts and symbols I use are the best way for me to illustrate my point, and I’ve included here a bit of a math lesson, in case it is not something you’ve encountered in your life – it will clarify some of the words and concepts I use for the rest of this article. Of course, if you feel there’s no need for you to read this section, by all means scroll past it and keep reading (I won’t feel bad).

Some Math concepts

Sets
Mathematicians like to talk about collections of values that are somehow related, and when they do, they use the word set. We use curly brackets to list the objects (known as elements) of a set. So for example the set F=\{apple, orange, banana, kiwi, peach, nectarine\} is a set I have named F, and just so you know, it is the set containing all the fruits I might bring to work with me in my lunch. A subset of a set S is another set that only contains elements from S. So for example M=\{apple, kiwi\} is the set of fruits I brought to work in my lunch on Monday, and is a subset of F. On the other hand, A=\{apple, pineapple, banana\} is not a subset of F.

A Little Bit of Algebra (Apologies to the Arithmophobic)
Consider this simple algebra equation:
\displaystyle 3x+4y=7
The x and y are understood to be symbolic of numbers, but the use of symbols mean that they vary – which is to say, they are variable. The equation is a statement. In this particular statement,
x = 1, y=1
would be a valid solution (i.e., the equation becomes true), since
3\times 1 + 4\times 1=7.
So would
x = 5, y=-2,
since
3\times 5 + 4\times (-2)=7.
However
x = 5, y=2
would not be a solution (i.e., the equation becomes false), since
3\times 5 + 4\times 2=23,
which is not 7.

Statements
In math and philosophy, a statement is a sentence that must either be true or false (but not both, and not maybe). Very often the truth value (i.e., “true” or “false”) of the statement depends on values for variables contained in the statement. The algebra equation above is a statement. Another example is the statement “I like cheese”, which contains two variables: “I”, and “cheese”. If the “I” refers to “Rich Dlin” (i.e., it is me speaking and not you), and the “cheese” refers to “Havarti”, then the statement is true. If the “I” is “Rich Dlin”, and the “cheese” is “Cambozola”, the statement (I promise you) is false. Notice that if the “cheese” were to refer to “gingerbread cookie” the statement would be nonsense, since “gingerbread cookie” is not a cheese – even though it is true that I like gingerbread cookies, it is irrelevant in the context of this statement. A mathematician would say “gingerbread cookie” is not an element of the set of all cheeses. Going back to the algebra example, {(1,1),(3,-2)} is a subset of the set of solutions to the equation given. The actual set has an infinite number of solutions in it, but that’s more than I need to talk about here. What I will say is that the truth value of the statement “Three times John’s favorite number plus four times Gail’s favorite number will yield seven” is:

True if (“John’s favorite number“, “Gail’s favorite number“) belongs to the set of solutions of 3x + 4y = 7,

False if (“John’s favorite number“, “Gail’s favorite number“) does not belong to the set of solutions of 3x + 4y = 7, and

Nonsense if, for example, John claims his favorite number is “cinnamon“. Be on the lookout for nonsense – it is surprisingly common.


The Assumptions
Ok. Welcome back. Here are the assumptions I was talking about:

All questions have a right answer …
… when the answer is justified properly with a well framed statement.
The truth value of the statement may be subject to variables that change which answer is correct, but with a fixed set of values for the variables, there is a right answer. For example, the question “Should all trees taller than 12 feet in our neighborhood be pruned?” could be answered “Yes”, justified with the statement “It is unacceptable for some trees in our neighborhood to block sight lines to the lakefront”. Note that here the answer to the question is “yes” if the statement is true, and “no” if the statement is false, and may reasonably depend on whether or not the tree is also so wide, or part of a grove, as to make it impossible for a resident to see the lakefront from a different angle standing on the same property. It may also depend on whether 12 feet is a reasonable height with respect to whether or not sight lines get blocked. In this case these variables need to be introduced into the statement, or else agreed upon as not being variable.

The right answer may well not be knowable …
 … even with the variable values fixed – which doesn’t mean there is no right answer!
As an example, consider the question “How many humans are alive on Earth right now?”

  • The number changes many times in a short span of time. So the truth value of the answer depends on what time it is indexed to.
  • The answer is subject to a definition of “alive”, and the answers to whether or not some organisms are living humans are in dispute.
  • “On” Earth needs to be defined. If I am in an airplane, am I on Earth? What if I am in low orbit?
  • However there is an answer, if we fix the variables.
  • There is currently no way, even with the variables fixed, to know the answer.

Knowing the truth is inherently valuable.
This is a big one. Many people demonstrate by their behavior that they do not adhere to this assumption. A simple example is the person who refuses to go to the doctor about a problem because they are afraid of what they might find out. In some ways, not wanting to know the truth is a human quality, especially in situations where a false belief has spawned an entire tree of values and beliefs we have been living by. If the root belief is false, what happens to the tree?

When it Comes to Truth, What We Want Doesn’t Matter
So with these assumptions, my position is that for any belief I hold, I am either right or wrong, and that I may not be able to tell. So then what am I to make of someone who disagrees? Can I immediately conclude that they are wrong? Clearly not. However I freely admit I want them to be wrong, so that I don’t have to be. After all, being wrong has some negative implications. On a fairly benign end it means I have been somehow deluded, which injures my pride. On an extreme end it may mean I have to discard an entire tree of conclusions that were premised on my error, leaving behind a buzzing hive of uncomfortable questions and observations about my previous behavior. But if the root belief is actually wrong, what choice do I really have? Since it is rooted in falsehood, the whole tree is an illusion anyway.

Here is a hard truth: What we want has nothing to do with what is true. I want there to be peace in the Middle East. But there is not peace in the Middle East, and no amount of wishing on my part, no matter how fervent, can alter the truth value of this or any other statement. On the other hand, what is true can and should definitely impact what I want. What we all want.

Ok. Here is another statement that is tautologically true: In the set of things I hold to be true, some might be false. And from a probability perspective, I am also comfortable saying that in the set of things I hold to be true, some are true, and some are false. I want to say “most are true and some are false”, but I am honestly not sure I have a reasonable argument to claim that, so we’ll leave it there as a desire more than a fact.

Shades of Gray
Now I will focus on statements where the truth depends on fixing values for the variables in the statement., which to me is the core of the shades of gray argument: In cases where there is a continuum of possibilities between true and false, almost everything in the set of things I hold to be true lies somewhere within the boundaries of the continuum, rather than on one of the ends.

Here a philosopher or mathematician might (and should!) argue that there can be no continuum between true and false, since those are binary options. My response is that I am talking about a sphere of reasonable answers centered on the truth, where anything outside the sphere is easily demonstrated to be false (or worse, nonsense), but things get a little more touchy inside the sphere. This is a consequence of my point about the truth of a statement depending on fixing values for variables the statement depends upon. To elaborate on this, I am going to define something called an assumption set.

Assumption Set
Suppose a statement depends on a set of variables. For example, consider the statement “Running is good for you.” The truth of this is not absolute. It depends on some variables:

  • How much running (the quantity of the running)?
  • How intense (the quality of the running)?
  • What preconditions do you have that running would exacerbate (e.g, bad knees, asthma, heart problems)?
  • Where do you plan to do your running (road, track, beach)?
  • and many more.

So before we could discuss whether the statement is true, we would have to fix values for these variables. I call these fixed values the assumption set. So for example an assumption set for this statement could be
R=\{45 minutes per day, at 80\% of maximum heart rate, \{sensitive to sunlight, plantar fasciitis\}, track\}.
Notice that one of the elements (the preconditions) in this assumption set is itself a set – that’s completely acceptable. On the whole, I would judge this assumption set to be a reasonable one – which is to say, the elements of the set have a probability associated with them that makes them not unexpected in the context of discussing the claim that “Running is good for you.”
Another assumption set could be
S=\{15 hours per day, at 120\% of maximum heart rate, \{multiple hip replacements, torn Achilles tendon\}, Interstate Highways\}.
On the whole, I would judge this assumption set to be very unreasonable – which is to say, it is highly improbable that this would be an assumption set on which the claim “Running is good for you” would be a relevant discussion.

Reasonable Answers (Approximately True?)
A reasonable answer to a question can be defined as a statement that is true when evaluated with a plausible assumption set. That is to say, the assumption set is comprised of elements that have probabilities high enough that if we observed them we would not be surprised. In situations where the variables are in constant flux, the approximate truth value of a statement may be argued as the one that holds given the most likely assumption set. In cases like this, we may generalize a statement as true, while being willing to challenge it in the face of a game-changing assumption set. We maybe won’t talk about who gets to define “plausible”, even though there are times when that becomes the most relevant thing.

Arguing(?) With an Open Mind
Here I have chosen to use the word “arguing”, even though in truth I prefer the word “discussing”. That’s because most people seem to think that discussions between people in disagreement need to be arguments. I disagree. Remember the assumption that we are not right about everything? And remember the assumption that knowing the truth is inherently valuable? These two should premise every discussion we enter into. So when discussing the answers to questions, or the truth about statements, we need to do our best to remember that what we are trying to do is get as close to the center of the sphere as possible, because that is a good thing to do, and because we may not be there yet.

Of course, we all think we are closer than an opponent. If not, we wouldn’t be having the discussion in the first place. But keeping in mind that if two people are in disagreement, one of them must be wrong, a productive conversation is one where at the end of it the parties have converged on something they both hold to be as close to true as they can see getting. When this happens, the world gets a win. I’ll list some techniques for true open-mindedness.

Discussing With an Open Mind

  1. Remember that you might be wrong.
    Put another way, be willing to change your mind, or adjust the approximate truth of what you believe.
    See, you believe that you are probably right. You may even believe that you are certainly right (although for the truly reflective, certainty is a pretty difficult thing to attain). But your opponent has the same thoughts. Both of you probably have many reasons for these. And they probably have a lot to do with assumption sets, and which one of you is applying the most plausible set. Sometimes the discussion is not about the truth of the statement but on the plausibility of the assumption set. Keep that in mind. Yours may be the less plausible. Or maybe both assumption sets are equally plausible, in which case the statement can be split into two (or more) more detailed statements that include some of the differing assumptions explicitly. But keep in mind that emotional attachment to an assumption set can and will blind you to the plausibility of an alternate set, and ultimately cause you to refute a statement with unreasonable (even fanatical) obstinacy.
  2. Have higher expectations for yourself than you do for your opponent.
    This means you need to challenge yourself to inspect the assumptions and claims of yourself and your opponent objectively, even if they are not doing the same thing. When you do this – and do it out loud – they hear that. Look at elements of the assumption sets and objectively evaluate their probability. Also evaluate whether they change the truth value of the statement or not. And be prepared to evaluate whether or not they render the statement as nonsense – this happens surprisingly often but it’s not obvious until it is isolated. Discussing things this way models a behavior that is necessary for the two of you to converge on a conclusion you both agree with. And if you are consistent with it, your opponent will often adopt the same style, if only because they think this is the way to convince you they are right.
  3. Thank your opponent, regardless of the outcome.
    I don’t mean this as a politeness. I mean this in the most sincere sense. Any opportunity we get to reflect on our set of beliefs is valuable. Sometimes your opponent and you will converge. Sometimes you will not, and they leave the exchange completely unmoved, perhaps even claiming “victory”. This is sad, since the only true victory would be a convergence of opinion, but ultimately it is not relevant to your own experience. Make it so that if you have moved on a topic, it is because you discovered something you were not considering, or were considering incorrectly, and now you are closer to the center of the sphere of truth. If you do not move, make it because you were not presented with any strong evidence that you needed to. In either case your beliefs will have been strengthened in some way, either because you changed to something as a result of new insight, or because you were challenged in some way, and it was unsuccessful. For this you have your opponent to thank.

How to Spot Real Open-Mindedness
Many people claim to be open-minded. It may be true, or it may be a trick (some people say it so that when you fail to convince them of something it will prove they were right). True open-mindedness doesn’t mean you are ready to believe anything. It means you are willing to change your mind when presented with evidence that objectively compels you to do so. If you know of (or are) someone who has changed their mind in the moment, during rational discourse, but who was fairly slow to do so, they are probably the type of person I am describing. This goes back to my point that we are probably not right about everything we believe. Which means mind-changing can occur. Which means if you’ve seen it occur, it occurred in someone with an open mind.

Thanks for reading,

Rich